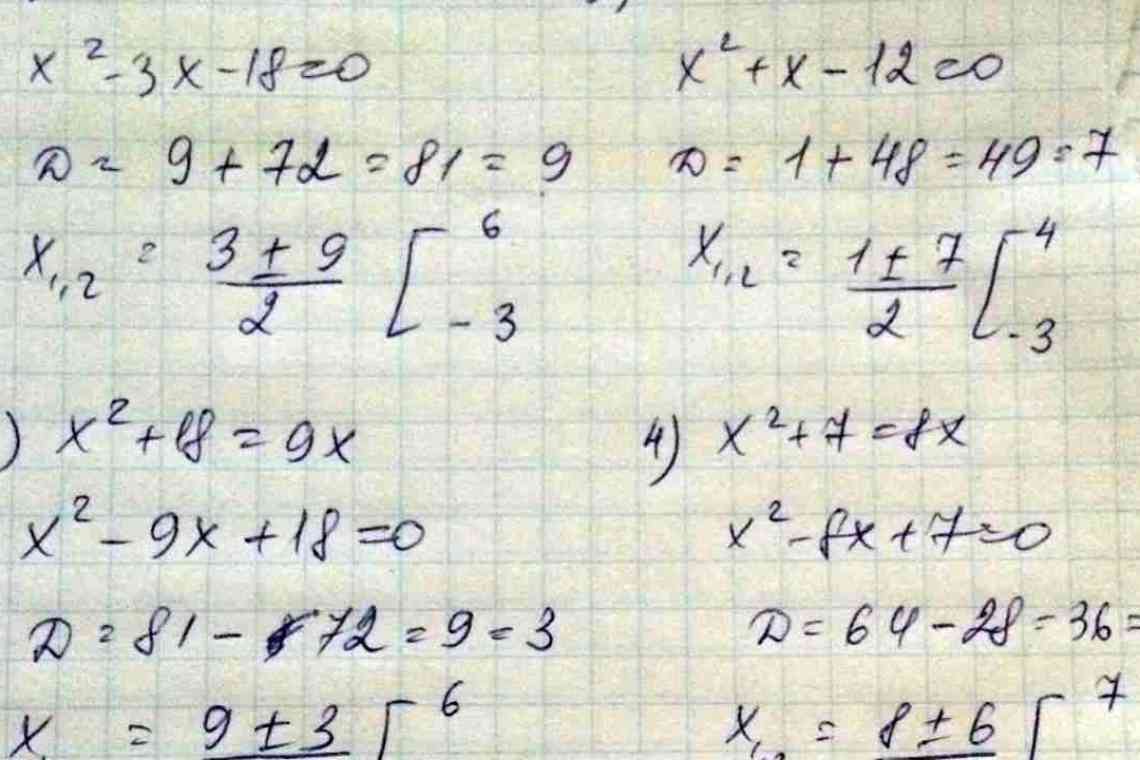Вивчаючи алгебру, школярі стикаються з рівняннями багатьох видів. Серед тих з них, які найбільш прості, можна назвати лінійні, що містять одну невідому. Якщо змінна математичного виразу зводиться до певного ступеня, то рівняння називають квадратним, кубічним, біквадратним тощо. Вказані вирази можуть містити раціональні числа. Але існують також рівняння ірраціональні. Від інших вони відрізняються наявністю функції, де невідоме знаходиться під знаком радикала (тобто чисто зовні змінну тут можна побачити написаною під квадратним коренем). Рішення ірраціональних рівнянь має свої характерні особливості. При обчисленні змінної для отримання правильної відповіді їх слід обов'язково враховувати.
«Невимовні слова»
Не секрет, що стародавні математики оперували переважно раціональними числами. До таких відносяться, як відомо, цілі, що виражаються через звичайні і десяткові періодичні дроби представники даної спільноти. Однак вчені Середнього і Близького Сходу, а також Індії, розвиваючи тригонометрію, астрономію і алгебру, ірраціональні рівняння теж вчилися вирішувати. Наприклад, греки знали подібні величини, але, облікаючи їх у словесну форму, вживали поняття «алогос», що означало «невимовні». Дещо пізніше європейці, наслідуючи їх, називали подібні числа «глухими». Від усіх інших вони відрізняються тим, що можуть бути представлені тільки у формі нескінченного неперіодичного дробу, остаточний числовий вираз якої отримати просто неможливо. Тому частіше подібні представники царства чисел записуються у вигляді цифр і знаків як певний вираз, що знаходиться під коренем другого або більшого ступеня.
На підставі вищесказаного спробуємо дати визначення ірраціональному рівнянню. Подібні вирази містять так звані «невиразні числа», записані з використанням знака квадратного кореня. Вони можуть представляти собою всілякі досить складні варіанти, але у своїй найпростішій формі мають такий вигляд, як на фото нижче.
Злочинляючи до вирішення ірраціональних рівнянь, першо-напершо необхідно обчислити область допустимих значень змінної.
Чи має сенс вираз?
Необхідність перевірки отриманих значень випливає з властивостей арифметичного квадратного кореня. Як відомо, подібний вираз прийнятний і має будь-який сенс лише за певних умов. У випадках кореня парної міри всі підкорінні вирази повинні бути позитивними або рівнятися нулю. Якщо ця умова не виконується, то поданий математичний запис не може вважатися осмисленою.
Наведемо конкретний приклад, як вирішувати ірраціональні рівняння (на фото нижче).
У даному випадку очевидно, що зазначені умови ні при яких значеннях, що приймаються шуканою величиною, виконуватися не можуть, так як виходить, що 11'x'4. А значить, рішенням може бути тільки ^.
Метод аналізу
З вищеописаного стає зрозуміло, як вирішувати ірраціональні рівняння деяких типів. Тут дієвим способом може виявитися простий аналіз.
Наведемо ряд прикладів, які знову наочно це продемонструють (на фото нижче).
У першому випадку при уважному розгляді виразу відразу виявляється гранично ясно, що істинним він бути не може. Дійсно, адже в лівій частині рівності має виходити позитивне число, яке ніяк не здатне виявитися рівним -1.
У другому випадку сума двох позитивних виразів може вважатися рівною нулю, лише коли х - 3 = 0 і х + 3 = 0 одночасно. А подібне знову неможливо. І значить, у відповіді знову слід писати.
Третій приклад дуже схожий на вже розглянутий раніше. Дійсно, адже тут умови ОДЗ вимагають, щоб виконувалася наступна абсурдна нерівність: 5 х - 2. А подібне рівняння аналогічним чином ніяк не може мати здорових рішень.
Необмежене наближення
Природа ірраціонального найбільш ясно і повно може бути пояснена і пізнана тільки через нескінченний ряд чисел десяткового дробу. А конкретним, яскравим прикладом з членів цього сімейства є. Не без підстав передбачається, що ця математична константа була відома з давніх часів, використовуючись при обчисленні довжин кола і площі кола. Але серед європейців її вперше застосували на практиці англієць Вільям Джонс і швейцарець Леонард Ейлер.
Виникає ця константа наступним чином. Якщо порівнювати різні за довжиною кола, відношення їх довжин і діаметрів в обов'язковому порядку дорівнює одному і тому ж числу. Це і є. Якщо висловити його через звичайний дріб, то приблизно отримаємо 22/7. Вперше це зробив великий Архімед, портрет якого представлений на малюнку вище. Саме тому подібне число отримало його ім'я. Але це не явне, а наближене значення чи не найдивовижнішого з чисел. Геніальний вчений з точністю до 0,02 знайшов шукану величину, але, по суті, дана константа не має реального значення, а виражається як 3, 1415926535... Вона являє собою нескінченний ряд цифр, необмежено наближаючись до якогось міфічного значення.
Зведення у квадрат
Але повернемося до ірраціональних рівнянь. Щоб відшукати невідоме, в даному випадку дуже часто вдаються до простого методу: зводять обидві частини наявної рівності в квадрат. Подібний спосіб зазвичай дає хороші результати. Але слід враховувати підступність ірраціональних величин. Всі отримані в результаті цього коріння необхідно перевіряти, адже вони можуть не підійти.
Але продовжимо розгляд прикладів і постараємося знайти змінні знову запропонованим способом.
Зовсім нескладно, застосувавши теорему Вієта, знайти шукані значення величин після того, як в результаті певних оперцій у нас утворилося квадратне рівняння. Тут виходить, що серед коріння будуть 2 і -19. Однак під час перевірки, підставивши отримані значення в початковий вираз, можна переконатися, що жоден з цих коренів не підходить. Це часте явище в ірраціональних рівняннях. Отже, наша дилема знову не має рішень, а у відповіді слід вказати порожню безліч.
Приклади складніші
У деяких випадках потрібно зводити в квадрат обидві частини виразу не один, а кілька разів. Розгляньмо приклади, де потрібно вказане. Їх можна побачити нижче.
Отримавши коріння, не забуваємо їх перевіряти, адже можуть виникнути зайві. Слід пояснити, чому таке можливо. При застосуванні подібного методу відбувається в деякому роді раціоналізація рівняння. Але позбуваючись неугодних нам коренів, які заважають проводити арифметичні дії, ми ніби розширюємо існуючу область значень, що загрожує (як можна зрозуміти) наслідками. Передбачаючи подібне, ми і проводимо перевірку. В даному випадку є шанс переконатися, що підходить тільки один з коренів: х = 0.
Системи
Що ж робити у випадках, коли потрібно здійснити вирішення систем ірраціональних рівнянь, і у нас в наявності не одне, а цілих два невідомих? Тут робимо так само, як у звичайних випадках, але з урахуванням перерахованих вище властивостей даних математичних виразів. І в кожному новому завданні, зрозуміло, слід застосовувати творчий підхід. Але, знову ж таки, краще розглянути все на конкретному прикладі, представленому нижче. Тут не просто потрібно знайти змінні х і у, а й вказати у відповіді їх суму. Отже, є система, що містить ірраціональні величини (див. фото нижче).
Як можна переконатися, подібне завдання не представляє нічого надприродно складного. Потрібно лише проявити кмітливість і здогадатися, що ліва частина першого рівняння являє собою квадрат суми. Подібні завдання зустрічаються в ЄДІ.
Ірраціональне математика
Щоразу потреба у створенні нових видів чисел виникала у людства тоді, коли йому не вистачало «простору» для вирішення якихось рівнянь. Ірраціональні числа не є винятком. Як свідчать факти з історії, вперше великі мудреці звернули на це увагу ще до нашої ери, століття в VII. Зробив це математик з Індії, відомий під ім'ям Манава. Він чітко розумів, що з деяких натуральних чисел неможливо витягти корінь. Наприклад, до таких належать 2; 17 або 61, а також багато інших.
Один з піфагорейців, мислитель на ім'я Гіппас, прийшов до того ж висновку, намагаючись виробляти обчислення з числовими виразами сторін пентаграми. Відкривши математичні елементи, які не можуть бути виражені цифровими значеннями і не володіють властивостями звичайних чисел, він настільки розлютив своїх колег, що був викинутий за борт корабля, в море. Справа в тому, що інші піфагорейці визнали його міркування бунтом проти законів всесвіту.
Знак радикала: еволюція
Знак кореня для вираження числового значення «глухих» чисел став використовуватися при вирішенні ірраціональних нерівностей і рівнянь далеко не відразу. Вперше про радикала почали замислюватися європейські, зокрема італійські, математики приблизно в XIII столітті. Тоді ж для позначення придумали задіяти латинську R. Але німецькі математики у своїх роботах надходили інакше. Їм більше сподобалася буква V. У Німеччині незабаром поширилося позначення V (2), V (3), що покликане було виражати корінь квадратний з 2, 3 і так далі. Пізніше в справу втрутилися нідерландці і видозмінили знак радикала. А завершив еволюцію Рене Декарт, довівши знак квадратного кореня до сучасної досконалості.
Визволення від ірраціонального
Ірраціональні рівняння та нерівності можуть включати змінну не тільки під знаком квадратного кореня. Він може бути будь-якої міри. Найпоширенішим способом від нього позбутися є можливість звести обидві частини рівності у відповідний ступінь. Це основна дія, що допомагає при операціях з ірраціональним. Дії в парних випадках особливо не відрізняються від тих, які були вже розібрані нами раніше. Тут повинні бути враховані умови неотрицьовості підкорінного виразу, а також після закінчення рішення необхідно проводити відсів сторонніх значень змінних таким чином, як було показано в розглянутих вже прикладах.
З додаткових перетворень, які допомагають знайти правильну відповідь, часто використовується множення виразу на сполучений, а також нерідко потрібно введення нової змінної, що полегшує рішення. У деяких випадках, щоб знайти значення невідомих, доцільно застосовувати графіки.